Lab3

Forberedelser

Les ukens kursnotater.
Les videre i kapittel 2 (alt frem til “importing modules”) i Automate the Boring Stuff with Python.
Les utforskning 3 med eksempler som er spesielt relevante for denne laben.

Innlevering og automatisk retting

Innlevering skjer via mitt.uib
For å få bestått, må du ha 100% riktig på CodeGrade
Du kan levere så mange ganger du vil. Siste innlevering telles.

Oppgave 1

I uke_03_oppg_1.py skriv en funksjon multiples_of_seven_up_to som tar en parameter n. Når funksjonen blir kalt, skal den skrive ut alle positive heltall mindre enn n som er delelig med 7.

For eksempel skal et kall til multiples_of_seven_up_to(49) skrive ut:

Oppgave 2

I denne oppgaven skal du skrive ut en gangetabell til skjermen.

I uke_03_oppg_2.py skriv en funksjon multiplication_table med en parameter n. Funksjonen skal skrive ut gangetabellen for alle tall fra og med 1 til og med $n$. Utskriften skal følge mønsteret vist under.

Eksempelkjøringer:

multiplication_table(3)

1: 1 2 3
2: 2 4 6
3: 3 6 9

multiplication_table(5)

1: 1 2 3 4 5
2: 2 4 6 8 10
3: 3 6 9 12 15
4: 4 8 12 16 20
5: 5 10 15 20 25

La funksjonen ha to nøstede løkker, som begge går igjennom verdiene fra 1 til n.
En iterasjon av den ytterste løkken er ansvarlig for å skrive ut én linje. Den ytterste løkken inneholder tre elementer: først, utskrift av hvilket tall denne linjen gjelder for, etterfulgt av kolon; deretter den innerste løkken; og til slutt utskrift av et linjeskift.
En iterasjon av den innerste løkken er ansvarlig for å skrive ut ett tall, nemlig produktet av iterandene (løkke-variablene) fra de to løkkene.
Husk at print(..., end=" ") vil skrive ut til skjermen og avslutte med et mellomrom istedet for et linjeskift.

Oppgave 3

I uke_03_oppg_3.py lag en funksjon dummy_chatbot uten parametere som snakker med brukere. Chatboten kan bare si tre ting: Hi! Do you want to talk to me?, That's cool!, eller All right, bye!. Du må bruke input() for å hente svar fra brukeren til chatboten.

Gjør et kall til dummy_chatbot() på slutten av filen. Dette er viktig for at CodeGrade skal klare å teste koden din.

Eksempler:

dummy_chatbot()

Hi! Do you want to talk to me?
yes   
That's cool!
Hi! Do you want to talk to me?
hello
That's cool!
Hi! Do you want to talk to me?
egentlig ikke
That's cool!
Hi! Do you want to talk to me?
no
All right, bye!

Denne oppgaven kan løses på flere måter, men siden vi ikke vet hvor mange ganger løkken skal kjøres på forhånd, må vi i alle tilfeller bruke en while-løkke.

Alternativ A: Du kan benytte en while True -løkke, og så benytte break dersom brukeren svarer no.
Alternativ B: Du kan opprette en variabel answer = "" før while -løkken starter, og la betingelsen for while-løkken være answer != "no".

Oppgave 4a

I filen uke_03_oppg_4.py skriv en funksjon cross_sum med en parameter n som returnerer tverrsummen av et gitt tall. Tverrsummen er summen av sifferne i tallet, for eksempel er tverrsummen av 12 lik 3, siden 1 + 2 = 3.

Test koden din ved å legge til disse linjene nederst i filen:

print("Tester cross_sum... ", end="")
assert(1 == cross_sum(1))
assert(3 == cross_sum(12))
assert(6 == cross_sum(123))
assert(10 == cross_sum(1234))
assert(10 == cross_sum(4321))
print("OK")

Du kan isolere det siste sifferet i et tall n med modulo-operasjonen n % 10 (for eksempel evaluerer 123 % 10 til 3).
Du kan fjerne det siste sifferet i et tall n med heltallsdivisjon n // 10 (for eksempel evaluerer 123 // 10 til 12).
Begynn med å opprette en variabel for tverrsummen, som i utgangsposisjon (før løkken starter) har verdien 0. Planen er å la dette være en løpende total, altså en variabel der vi adderer inn nye verdier flere ganger.
Så lenge tallet n er større enn 0: isoler det siste sifferet og legg det til i tverrsummen. Fjern så det siste sifferet fra n og fortsett med en ny iterasjon.

Oppgave 4b

I filen uke_03_oppg_4.py skriv en funksjon nth_number_with_cross_sum_x(n, x) som returnerer det n’te tallet hvor tverrsummen av tallet er x.

Det første tallet med tverrsum 7 er bare tallet 7, mens det andre tallet med tverrsum 7 er 16. Derfor skal nth_number_with_cross_sum_x(1, 7) returnere 7, mens nth_number_with_cross_sum_x(2, 7) skal returnere 16.

Test koden din ved å legge til disse linjene nederst i filen:

print("Tester nth_number_with_cross_sum_x... ", end="")
assert(7 == nth_number_with_cross_sum_x(1, 7))
assert(16 == nth_number_with_cross_sum_x(2, 7))
assert(25 == nth_number_with_cross_sum_x(3, 7))
assert(19 == nth_number_with_cross_sum_x(1, 10))
assert(28 == nth_number_with_cross_sum_x(2, 10))
assert(37 == nth_number_with_cross_sum_x(3, 10))
assert(2000 == nth_number_with_cross_sum_x(10, 2))
print("OK")

Merk: i denne oppgaven vet du ikke før løkken starter hvor mange iterasjoner løkken skal ha. Derfor bør du velge en while-løkke, og ikke en for-løkke.

Generelt hint: les alltid gjennom kursnotatene før du begynner på lab’en!

Oppgave 5

Et 1D linjestykke langs x-aksen begynner i punktet $x_\text{lo}$ og slutter i punktet $x_\text{hi}$. I filen uke_03_oppg_5.py skriv en funksjon split_line som deler opp et linjestykke i n like lange biter.

La funksjonen ha som parametre x_lo, x_hi samt et positivt heltall n. Funksjonen skal skrive ut n linjer, hver med to tall som representerer et linjestykke. For eksempel, et kall til split_line(1.0, 7.0, 3) skal skrive ut:

1.0 3.0
3.0 5.0
5.0 7.0

og et kall til split_line(0.0, 1.0, 4) skal skrive ut:

0.0 0.25
0.25 0.5
0.5 0.75
0.75 1.0

Merk: i denne oppgaven vet du allerede før løkken starter hvor mange iterasjoner løkken skal ha (nemlig n). Derfor bør du velge en for-løkke, og ikke en while-løkke. I denne oppgaven kan faktisk det å velge en while-løkke, i kombinasjon med avrundingsfeil som alltid vil skje når vi jobber med flyttall, gjøre at du får feil svar!

Legg merke til at lengden på hvert linjestykke blir $$b = \frac{x_\text{hi} - x_\text{lo}}{n}$$

Det første linjestykket begynner i $x_\text{lo} + b \cdot 0$ og slutter i $x_\text{lo} + b \cdot 1$.
Det andre linjestykket begynner i $x_\text{lo} + b \cdot 1$ og slutter i $x_\text{lo} + b \cdot 2$.
…og så videre

Oppgave 6a

I matematikken kan en funksjon for eksempel være definert som $g(x) = \frac{1}{8}x^2 - 2x + 10$. La oss modellere denne matematiske funksjonen som en programmeringsfunksjon:

I filen uke_03_oppg_6.py, opprett en funksjon g som har en parameter x og som regner ut verdien av $\frac{1}{8}x^2 - 2x + 10$ for den gitte verdien av x.

For eksempel skal et kall til g(8.0) returnere verdien 2.0, og et kall til g(4.0) skal returnere verdien 4.0.

def almost_equals(a, b):
    return abs(a - b) < 0.0000001

print("Tester g... ", end="")
assert(almost_equals(2.0, g(8.0)))
assert(almost_equals(4.0, g(4.0)))
assert(almost_equals(10.0, g(0.0)))
print("OK")

Oppgave 6b

I denne oppgaven skal vi regne ut en tilnærming for arealet under funksjonen $g$ (fra oppgave a) mellom to gitte punkter $x_\text{lo}$ og $x_\text{hi}$ på x-aksen. Vi antar at $x_\text{lo} \leq x_\text{hi}$, og i denne omgang antar vi også at $x_\text{lo}$ og $x_\text{hi}$ er heltall.

For å gjøre vår tilnærming, skal vi enkelt nok regne ut summen av g(x_i) for alle heltalls-verdier $x_i$ fra og med $x_\text{lo}$ opp til (og ikke inkludert) $x_\text{hi}$. For eksempel, dersom $x_\text{lo} = 3$ og $x_\text{hi} = 7$, er vi interessert i å vite hva summen $g(3) + g(4) + g(5) + g(6)$ blir.

I filen uke_03_oppg_6.py, opprett en funksjon approx_area_under_g med parametre x_lo og x_hi som returnerer summen av g(x_i) for alle heltall x_i fra og med x_lo opp til x_hi.

Arealet under grafen (til venstre) versus en tilnærmet utregning (til høyre)

print("Tester approx_area_under_g... ", end="")
assert(4.0 == approx_area_under_g(4, 5))   # g(4)
assert(3.125 == approx_area_under_g(5, 6)) # g(5)
assert(7.125 == approx_area_under_g(4, 6)) # g(4) + g(5)
assert(23.75 == approx_area_under_g(1, 5)) # g(1) + g(2) + g(3) + g(4)
print("OK")

På samme måte som i oppgave 4a trenger vi en variabel for vårt løpende totalareal.
Benytt en for-løkke som starter i x_lo og som går opp til x_hi

Oppgave 6c

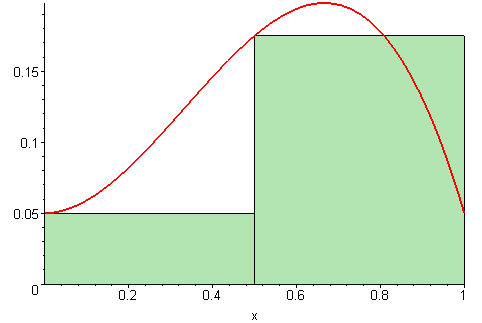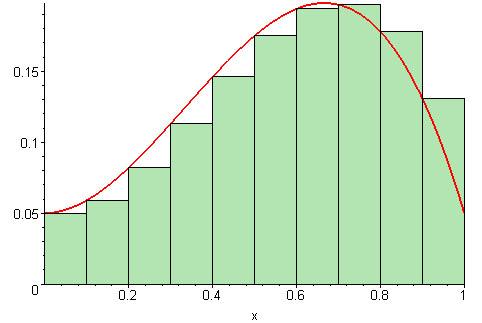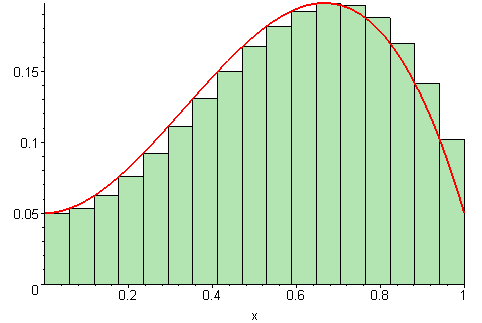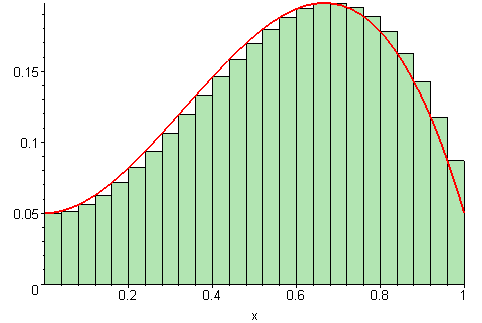
Estimatet for arealet vi regnet ut i forrige deloppgave er bare et estimat, siden vi later som funksjonen går i “trapper” i stedet for å være kontinuerlig, slik den egentlig er. For å gjøre estimatet vårt bedre, kan vi redusere “bredden” på hvert trappetrinn. Jo smalere trappetrinn vi velger, jo bedre blir estimatet vårt for arealet.

På figuren under vises det ulike bredder på trappetrinnene. Jo flere trappetrinn, jo mer nøyaktig vil arealet av det grønne området (som vi regner ut) stemme med det faktiske arealet under grafen (den røde streken).

Illustrasjon av 09glasgow09, CC BY-SA 3.0.

I denne oppgaven skal vi forbedre estimatet for arealet under grafen ved å la dem som kaller funksjonen vår bestemme hvor mange trappetrinn de ønsker å benytte. Dette kalles en (venstresidet) Riemann sum.¹

I filen uke_03_oppg_6.py, opprett en funksjon riemann_sum_g med parametre x_lo, x_hi og n. Funksjonen skal returnere en tilnærming av arealet under grafen g fra oppgave a basert på n antall trappetrinn.
På samme måte som i oppgave 4a og 6b skal vi oppdatere en løpende total i en løkke.
På samme måte som i oppgave 5 skal vi dele opp linjestykket $[x_\text{lo}, x_\text{hi}]$ i $n$ like store biter.

Merk: i denne oppgaven vet du allerede før løkken starter hvor mange iterasjoner løkken skal ha (nemlig n). Derfor bør du velge en for-løkke, og ikke en while-løkke. I denne oppgaven kan faktisk det å velge en while-løkke, i kombinasjon med avrundingsfeil som alltid vil skje når vi jobber med flyttall, gjøre at du får feil svar!

Legg merke til at hvert trappetrinn har bredde $b = ({x_\text{hi} - x_\text{lo}})/{n}$.
Observer at trappetrinn nummer $i$ begynner på x-verdien $x_i = x_\text{lo} + b \cdot i$. Det første trappetrinnet har nummer 0. Ergo begynner det første trappetrinnet ved $x_\text{lo}$, det andre trappetrinnet begynner ved $x_\text{lo} + b$, det tredje deretter begynner ved $x_\text{lo} + 2b$ og så videre.
For å regne ut arealbidraget fra trappetrinn $i$, multipliser bredden $b$ med verdien du får fra g(x_i).

print("Tester riemann_sum_g... ", end="")
assert(almost_equals(7.125, riemann_sum_g(4, 6, 2)))
assert(almost_equals(6.71875, riemann_sum_g(4, 6, 4)))
assert(almost_equals(6.3348335, riemann_sum_g(4, 6, 1000)))

assert(almost_equals(23.75, riemann_sum_g(1, 5, 4)))
assert(almost_equals(22.4375, riemann_sum_g(1, 5, 8)))
assert(almost_equals(21.166676666, riemann_sum_g(1, 5, 1_000_000)))
print("OK")

Oppgave 6d

Vi ønsker nå å regne ut arealet under flere grafer. Når alt kommer til alt er funksjonen $g(x) = \frac{1}{8}x^2 - 2x + 10$ relativt obskur.

Opprett en funksjon riemann_sum med parametre f, x_lo, x_hi og n. Funksjonen skal returnere en tilnærming av arealet under grafen f mellom x_lo og x_hi basert på n antall trappetrinn. Koden vil være helt identisk med forrige deloppgave, bortsett fra at du kaller f(x_i) istedet for g(x_i) inne i løkken.

For å teste funksjonen, legg denne koden nederst i filen:

# Vi sjekker først at riemann_sum med funksjonen g som argument gir
# samme svar som riemann_sum_g -metoden fra forrige deloppgave.
print("Tester riemann_sum med funksjonen g... ", end="")
assert(almost_equals(7.125, riemann_sum(g, 4, 6, 2)))
assert(almost_equals(6.71875, riemann_sum(g, 4, 6, 4)))
assert(almost_equals(6.3348335, riemann_sum(g, 4, 6, 1000)))

assert(almost_equals(23.75, riemann_sum(g, 1, 5, 4)))
assert(almost_equals(22.4375, riemann_sum(g, 1, 5, 8)))
assert(almost_equals(21.166676666, riemann_sum(g, 1, 5, 1_000_000)))
print("OK")

# Så tester vi med et par andre funksjoner
# Funksjonen som kvadrerer, square(x) = x**2
def square(x):
    return x**2

## Arealet under grafen square(x) = x**2 mellom 1 og 3
## Eksakt svar  er 8 + 2/3, altså 8.66666666....
## Merk at vi kommer gradvis nærmere eksakt svar ved å øke n
print("Tester riemann_sum med funksjonen square... ", end="")
assert(almost_equals(5.0, riemann_sum(square, 1, 3, 2)))
assert(almost_equals(7.88, riemann_sum(square, 1, 3, 10)))
assert(almost_equals(8.5868, riemann_sum(square, 1, 3, 100)))
print("OK")

# Funksjonen som er en jevnt stigende, linear(x) = x
def linear(x):
    return x

## Arealet under grafen for funksjonen f(x) = x mellom 2 og 4
## Eksakt svar er 6.
## Merk at vi kommer gradvis nærmere riktig svar ved å øke n
print("Tester riemann_sum med funksjonen linear... ", end="")
assert(almost_equals(5.0, riemann_sum(linear, 2, 4, 2)))
assert(almost_equals(5.5, riemann_sum(linear, 2, 4, 4)))
assert(almost_equals(5.998046875, riemann_sum(linear, 2, 4, 1024)))
print("OK")

Spesielt interesserte kan lese mer om ulike varianter av Riemann sum på Wikipedia. ↩︎